MARIN – System Parameter Identification in Numerical Simulations #SWI2014

A common problem in numerical simulations is finding the correct parameter values of a mathematical model. A typical example from MARIN practice is the simulation of a ship manoeuvre, like a zig-zag or a turning circle (Figure 1), where the result is compared with the outcome of an experiment. The forces acting on the ship are calculated with a mathematical model which has a number of tuning parameters. The question then is: which parameter values give the best result?

For a single simulation (like a zig-zag or a turning circle) this boils down to solving an optimization problem as shown in Figure 2. The ‘behaviour’ of the experiment (physical or numerical) is determined by the function \(F\), representing the real physics or the corresponding (complex) mathematical model, and the (input) control signal \(u\). The behaviour of the simulation is determined by the function \(\widetilde{F}\), representing the simpler mathematical model, and u. Various optimization techniques are available for the determination of the parameters \(p\) which make the difference between the simulated realisation \(\widetilde{x}\) and the experimental realisation \(x\) minimal.

Figure 1: Zig-zag (left) and turning circle (right) manoeuvres

A more difficult problem is finding parameter values with a larger validity range, allowing for multiple simulations, such as a combination of a zig-zag and a turning circle or a complex manoeuvre in a harbour with waves and current. The broader question then is: Which basic control signals and which parameter values must be chosen for an optimal result for a class of realisations? Ideally, the optimization procedure has a component which ‘measures’ both the experimental behaviour and the simulated behaviour and which makes a comparison. The goal is to find optimal parameter values using a limited set of control signals.

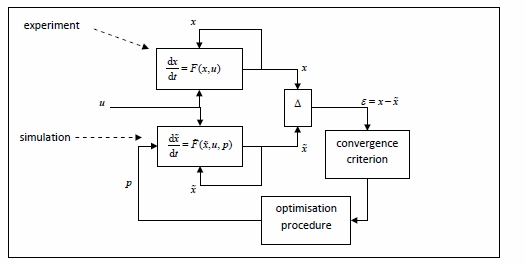
Figure 2: Parameter identification scheme