INCAS3 – Nonlinear Cochlear Mechanics #SWI2014
It is perhaps astonishing that in spite of the advances in medical imaging and other research techniques, the possibilities of visualizing damage to the human hearing system are very limited. Although there is a vast range of audiological tests that measure the effect of damage, pinpointing what is causing these effects is often impossible. This, unfortunately, results in a wide variety of hearing problems reported by people with very similar results on the audiological tests, and the corresponding uncertainty in estimating what is the best way to compensate for the hearing loss (see e.g. the development of ‘fitting-rules’ for estimating the required gain in hearing aids).
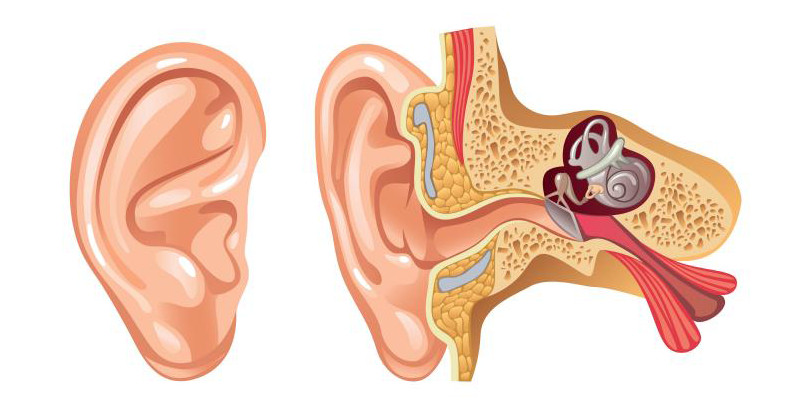
The reason for this is that the inner ear, where the conversion of movement to electrical impulses takes place, is very sensitive and vulnerable. For this reason, it is encased in the toughest bone in the human body, making it highly inaccessible. Measurements of cochlear action in vivo are scarce and can only be conducted in a small area of the cochlea of certain rodents. Insights into the mechanisms responsible for human hearing therefore heavily depend on models.
One such model was developed in cooperation between the departments of Biophysics and Applied Mathematics at Groningen University. This model simplifies the snail-shell shape of the cochlea to a rectangular box with the only longitudinal motion of the fluid and represents the organ of Corti (containing the hair cells that perform the mechano-electrical conversion) as a number (~400-1000) of individual sections behaving as harmonic oscillators. The excitation \(\zeta\) of each section is governed by an equation of motion of the shape:
$$ p =m\ddot{\zeta} + d\dot{\zeta} + s\zeta\tag{1}$$
where \(m\) is the mass of the section, \(s\) a stiffness restoring the section to its resting position and \(d\) a damping term. The driving force is represented by \(m\) and is fluid pressure. All oscillators are coupled via mass elements, representing an incompressible and inviscid fluid in the cochlear channels.
It was soon realized that this representation oversimplifies the mechanics of the organ of Corti, and in 1991 an additional term was introduced in the equation of motion:
$$ p =m\ddot{\zeta} + d\dot{\zeta} + s\zeta + s^{\prime}\zeta_{t-\tau}\tag{2}$$
allowing realistic simulations of a wide range of experimental data (see Epp et al).
A problem remaining is the estimation of the values of \(m\), \(d\), \(s\) and \(s^{\prime}\). The problems with accessibility and vulnerability of the cochlea prevent measurements in vivo. Therefore the values are mostly found using fitting procedures and estimated guesswork. An additional complicating factor is the strongly nonlinear mechanics of the cochlea. In order to be able to code the impressive range of 120 dB covered by human hearing in nerve cells with a dynamic range of only about 40 dB, the cochlea contains a compressive nonlinearity. It is thought that at low input levels and active process amplifies the motion of the cochlear partition to increase the sensitivity of our hearing. Although there are tell-tale signs of such an amplification mechanism and including it in models leads to realistic results, the fact that direct measurement of hair cell motion is impossible still leaves room for a heated debate about its existence.
One of the strongest indicators of the ‘cochlear amplifier’ and a possible way to gain more insight into cochlear damage is found in OtoAcoustic Emissions (OAEs). These are thought to be byproducts of the amplification process measurable in the ear canal as weak sounds emanating from the cochlea. The nonlinearity of the mechanics of the cochlea can be used to separate the emissions from the stimulus evoking them, e.g. in the case of DPOAEs the stimulus consists of the sum of two sinusoids with frequencies \(f_1\) and \(f_2\) and the emission contains components at intermodulation frequencies \(m f_1 + n f_2\) with \(n\) and \(\)m[\latex] positive or negative integer numbers.
The question we pose is whether it is possible to use (any combination of) OAE data to derive the shape of the mechanical cochlear nonlinearity.
Any information on the nonlinearity in the cochlea may help to improve the model, leading to a better quantitative match between OAE and other measurements that may help to assess hearing damage. Also, information on the nonlinearity required in the model to achieve this better match may give tantalizing clues about the relationship between the simplified mechanics as represented by equation (2) and the micromechanics of the organ of Corti in the real cochlea.