Thales – Optimization of the Lifetime of Sensor Networks #SWI2012
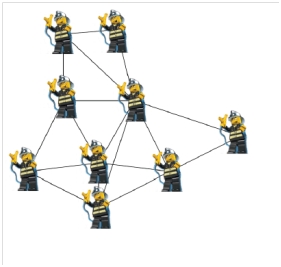
Sensor networks and networks of wearable communication systems (for example networks that support emergency workers in their efforts) have strong requirements for their energy consumption. Instead of only focusing on minimization of energy consumption of the individual nodes (which leads to locally optimal solutions) it is important to maximize the lifetime of the whole network.
Mathematically, we define the network lifetime as the time until the first node runs out of energy. It depends on the assigned transmit powers and the routing algorithm. For the network lifetime, analyses have been with simplified battery models. These models assume that the remaining energy in a battery is reduced with a fixed amount per data transmission (“the linear approach”). In reality, most batteries are non-ideal energy reservoirs and exhibit a battery recovery effect. The recovery effect implies that a battery recovers part of its capacity when given enough time between usage bursts.
The general question is: what are good practically useful energy prediction algorithms, transmit power assignment, and routing algorithms that maximize the network lifetime, taking into account the non-linear rate capacity and recovery effect of the involved batteries.
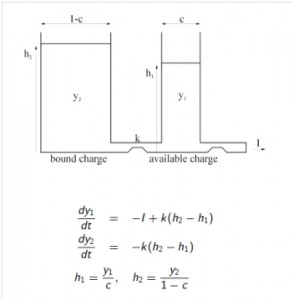
For the SWI we consider both linear and non-linear node-and battery models taking the “Optimized Link State Routing”- protocol is taken as a basis. OLSR optimizes the flooding of link state information through the network by using multipoint relays (MPRs). Only nodes selected as MPRs are responsible for forwarding control traffic. Within the protocol, each node has the possibility to indicate its ‘willingness’ to relay packets from other nodes. When we assume that ‘willingness = remaining battery capacity’, we can use the willingness to influence the MPR selection mechanism so that it selects ‘better’ MPRs. ‘Better’ means: leading to longer network lifetimes. We already discussed the linear battery model. For the nonlinear battery model, we propose to use the KiBAM model, describing the discharging of a battery by differential equations.
We propose the following questions, ranging from theoretical to practical:
Question 1. Selecting MPRs to maximize the minimum willingness is a heuristic. What would be the optimal MPR selection algorithm? With a linear battery decrease model, it should be possible to formulate this as a linear program. How much does the optimal solution differ from the heuristic?
Question 2. Assume a node can choose between different power levels. For each increasing level, each node will have larger sets of neighbors to choose the MPR from. Can we formulate the optimization problem and find some good heuristic to solve this (a solution is an assignment of transmit powers and MPR sets). What would be the impact on the network’s lifetime?
Question 3. Suppose that we know the MPR sets (selected in one way or another). The OLSR protocol allows us to assign weights to edges. OLSR will then calculate the minimum weight route from source to destination (which then of course only uses nodes from selected MPR sets). The question becomes: how should we assign the weights to get maximum network lifetime, taking into account the recovery effect as predicted by the KiBAM model?