SKF – Weibull Estimation of Bearing Performance from Acceptance Tests #SWI2018
 |
SKF is the world-leading supplier of products and solutions in the rolling bearing business. Bearing performance is assessed via intensive life testing and physical modeling. Beyond that, customers may require specific acceptance tests in the specific operating conditions from their application. Acceptance tests are usually dealing with a limited sample size meant to survive a test under severe conditions. To avoid being too conservative, acceptance tests may also be passed with very limited failures (1 or 2), making then the statistical estimation of the life parameters (the 10th life percentile) more challenging. When using a Weibull distribution, for instance, the shape parameter has to be assumed in order to keep reasonable confidence intervals. It is therefore needed to evaluate the risk taken while assuming the value of the shape parameter. In addition, the traditional (Nelson) approach for the estimation needs also to be assessed when the test data deviate from the Type II scheme (all censored data at the time of the last failure).
The problem proposed by SKF is then to assess the accuracy of the estimation while using Nelson’s approach to small data set (in particular when there are uncertainties on the value assumed for the shape parameter) and potentially to propose an alternative approach seized to the specific problem and range of data.
Let us take an example to illustrate the context:
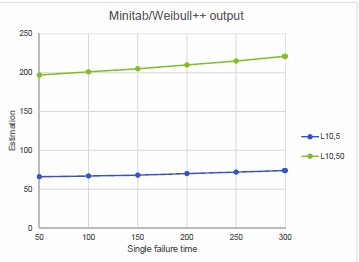
- Test on 6 bearings up to a maximum time of 300 hours
- One failure occurred at X hours (\(X= 50, 100, 150, 200, 250,
300\)), all other 5 bearings survived 300 hours - Assumed shape parameter \(\beta=1.5\)
Needed output:
- L10 median estimate (L10,50)
- L10 lower bound of the 90% two-sided confidence interval (L10,5)
Traditional method:
Other commercial software gives a “step” at X=300 hours for the lower bound (L10,5=106 hours).
Problems to address:
- How to explain/justify the very low sensitivity to X value?
- With low X (like 50h), is the method accurate?
- How to assess the confidence in the assumed shape parameter?
- Which alternative method could be used to estimate L10 (keeping the Weibull assumption)?
- Is it possible to set-up a different estimation method with boundaries (on the data set) to select the most appropriate one?