DNV GL – Stability Analysis of a Buck Converter in Feedback Control #SWI2018

DNV GL in brief

DNV GL is a global quality assurance and risk management company. Driven by our purpose of safeguarding life, property, and the environment, we enable our customers to advance the safety and sustainability of their business. We provide classification, technical assurance, software, and independent expert advisory services to the maritime, oil & gas, power, and renewables industries. We also provide certification, supply chain, and data management services to customers across a wide range of industries. Combining technical, digital, and operational expertise, risk methodology, and in-depth industry knowledge, we empower our customers’ decisions and actions with trust and confidence. We continuously invest in research and collaborative innovation to provide customers and society with operational and technological foresight. With origins stretching back to 1864 and operations in more than 100 countries, our experts are dedicated to helping customers make the world safer, smarter, and greener.

Problem description

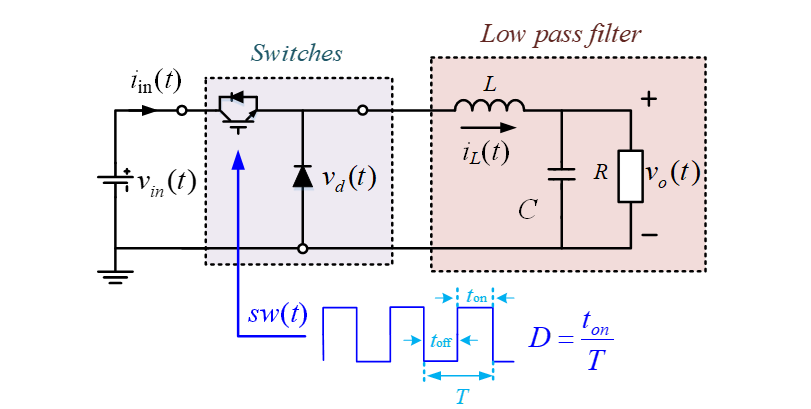
The problem is to find sufficient stability conditions for the solution of a set of nonlinear differential equations with discontinuous coefficients in feedback, which comes from the stability of a feedback control loop aiming to stabilize the output voltage of a buck converter.
The system is partially defined by the set of equations

\begin{eqnarray}
\dot{i}(t) &=& \frac{1}{L} \left(s(t) v-v_o(t)\right),\\
\dot{v}_o(t) &=& \frac{1}{C} \left(i(t)-\frac{v_o(t)}{R(t)}\right),\\
s(t) &=& \sum_{k=1}^\infty \delta((k-D(t))T < t \leq kT)
\end{eqnarray}

where \(i(t)\) is the current flowing through the circuit, \(T\) , \(L\) and \(C\) are positive constants, \(s(t)\) is a \(0\) –\(1\) switching signal, \(v\) is the input voltage, and \(v_o(t)\) is the voltage over the time dependent positive load \(R(t)\) . The function \(D(t) \in [0,1]\) is the duty ratio signal of the converter which shows that in a short interval of length \(T\) the switching signal \(s(t)=1\) in the last \(D(t)T\) part of the interval. (\(T=1\) can be fixed for normalization.)

The goal of the converter is to keep its output voltage \(v_0(t)\) constant at a prescribed level. The control is carried out by a feedback mechanism monitoring \(v_0(t)\) and adjusting the duty cycle ratio \(D(t)\).

DNV-GL is looking for a methodology that allows them to verify the stability of the converter given some control algorithm that generates \(D(t)\) based on \( v_0(t)\) under the assumption that \(R(t)\) is a discontinuous function with jumps.

Stability is understood as \(v_o(t)\) should not have big oscillations and those oscillations should attenuate fast.